브루트 포스

정의

브루트포스는 모든 경우의 수를 다 해보는 것이다.

예시

비밀번호가 4자리고 숫자로만 이루어져 있으면 000부터 9999까지 입력해보면된다. 경우의수가 10000가지. 이때 각 1초가걸린다면 10,000초 = 2.7시간 소요.

유의할 점

먼저 가능한 방법의 수를 세본다. 이 떄, 경우의 수를 다해보는데 걸리는 시간이 문제의 시간제한을 넘지 말아야 한다. 넘지않으면 브루트포스로 푸는 문제. 아니면 브루트포스로 풀면안된다.

• 3단계
  1. 문제의 가능한 경우의 수를 계산해본다. -> 직접계산을 통해 구한다. 대부분 손으로 계산해볼 수 있다.
  2. 가능한 모든 방법을 다 만들어본다. -> 하나도 빠짐없이 만들어야 한다. -> 대표적으로 그냥 다해보는방법, for문사용, 순열사용, 재귀호출 사용, 비트마스크 사용이 있다. (문제마다 좋은 방법이 다름)
  3. 각각의 방법을 통해 답을 구해본다.

예시

비밀번호가 12자리고 숫자로만 이루어져 있으면 000000000000부터 999999999999까지 입력해보면된다. 경우의수가 1000000000000가지. 이때 각 1초가걸린다면 1000000000000초 = 약 31688년 소요.

시간복잡도

O(방법의수 x 방법 1개의 시간복잡도)

경우의수

1. N명의 사람이 한 줄로 서는 경우의 수 -> n!
2. N명의 사람 중에서 대표 두 명을 뽑는경우 ->nC2 = n(n-1)/2
3. N명의 사람중에서 대표 세 명을 뽑는경우 -> nC3 = n(n-1)(n-2)/3!
4. n명의 사람중에서 반장 1명과 부반장 1명을 뽑는 경우의 수 -> n*(n-1)
5. N명의 사람이 있을때 각 사람이 영화를 볼지, 보지 않을지 결정한다. 가능한 조합의수 -> 2의n제곱

• 정확히 계산안해도 n제곱인지 n세제곱인지 등 아는것이 중요!

해결법

브루트포스에서 해결하는 방법은 크게 3가지로 나누어진다.

1. 재귀법 **
2. 순열
3. 비트마스크

여기서 재귀가 가장 중요하다. 순열,비트마스크는 재귀로도 해결가능하기 때문이다.

재귀를 사용하는 브루트포스는 크게 2가지로 나누어진다. 1.순서관련 문제 ex) boj15649 N과 M(1) 2.선택관련 문제 ex) boj15649 N과 M(2)

브루트포스 - 순열

순서가 매우 중요한 경우 사용하는 기법

순열?

임의의 수열을 다른 순서로 섞는 연산 크기가 N인 수열의 서로 다른 수열은 총 N!개 있다.

---

예) A = [1,5,6]인 경우 [1,5,6], [1,6,5],[5,1,6],[5,6,1],[6,1,5],[6,1,6]이 순열이다.

---

다음 순열 구하는 algrotihm은 C++, Python등에는 library가 구현되어있지만 java는 없어서 직접구현하자.

---

백트래킹이란?

백트래킹은 완전탐색과 매우 유사한 알고리즘이다.

-차이점 브루트포스 : 모든 경우의 수를 대입해보며 정답을 확인하는 작업

백트래킹 : 완전탐색을 개선한 기법. 후보 해들을 단계적으로 만들어 가는 과정에서 후보 해들을 평가. 만약 한 후보 해가 최종 해가 될 수 없다고 판단되면 탐색을 멈추고 다른 후보 해를 탐색

비트마스크

비트연산 종류

&(and), |(or), ~(not), ^(xor) «(shift left), »(shift right)

• A«B (A를 왼쪽으로 B비트만큼 민다.) 1 « 0 = 1 1 « 1 = 2 (10(2)) 1 « 2 = 4 (100(2)) 1 « 3 = 9 (1000(2)) 1 » 0 = 1 1 » 1 = 0 10 » 1 = 5 (101(2))

즉, A«B = A*2의B승 A»B = A/2의B

연산

두 수 A와 B를 비트연산하는 경우에는 가장 뒤의 자리부터 하나씩 연산을 수행하면 된다.

연산속도

o(1)이다.

주의

not 연산의 경우에는 자료형에 따라 결과가 달라진다. A = 83 = 101001 (2) ~A = 10101100 (2) (8비트 자료형인경우) ~A = 1111111 11111111 11111111 10101100(2) (32비트 자료형인경우)

또 unsigned, signed에 따라서 보여지는 값은 다르다. (c++경우)

주의2

연산자 우선순위 조심해야한다. ex) 1 « N-1이면 (1 « N) -1인지 1 « (N - 1)인지 괄호를 표기해야한다.

그래서 비트마스크?

정수로 집합을 나타낼 수 있다!

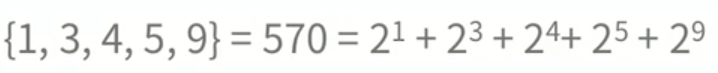
• 장점
  1. 공간절약
  2. 정수라는 것이 장점 배열의 인덱스 같은것으로 활용가능 A[570] 은 가능하지만 A[{1,3,4,5,7}]은 안된다.

주의3

사용할때 이 집합에 들어갈 수 있는 최대값을 알아야한다. int는 32비트라 2의32승 넘는 정보는 저장할 수 없다.

주의4

보통 0부터 N-1까지 정수로 이루어진 집합을 나타낼때 사용 -> 1부터 N까지 정수로 이루어진 집합을 사용하는건 공간이 2배 더필요하다. (0부터 1까지 1비트까지 더필요하므로 전체는 2배) -> 따라서 연산을통해 조금 변형해서 사

포함 확인 예시

{1, 3, 4, 5, 9} = 570 1) 0이 포함되어있나 검사 570 & 2의0승 = 570 & (1«0) = 0 2) 1이 포함되어있나 검사 570 & 2의1승 = 570 & (1«1) = 2 3) 2가 포함되어있나 검사 570 & 2의2승 = 570 & (1«2) = 0

추가 예시

{1,3,4,5,9} = 570 1) 1 추가하기 570 | 2의1승 = 570 | (1«1) = 570 (1000111010)

제거 예시

{1,3,4,5,9} = 570 1) 1제거하기 570 & ~2의1승 = 570 & ~(1«1) = 568

토글 예시

{1,3,4,5,9} = 570 1) 1 토글하기 570 ^ 2의1승 = 570 ^ (1«1) = 568

그 외

1) 전체 집합 (1 « N) - 1 = 2의N승 -1

2) 공집합 0